水平思考的目的在于,以不同方式看待事物、重组模式、生成更多方案。
有时候,心怀生成不同方案的意愿就很好,因为你能停下来多看看,避免一条道走到黑。但更多时候,仅有意愿还远远不够,你还需要借助一些实际方法。
在大脑的记忆系统中,模式一旦形成,就会不断扩大、延伸和组合,形成新的模式,而新模式之后也会得到独立应用。模式的整体性越强,重构的难度就越大。因此,如果多个模式组合成新模式,要换一种视角来剖析就会更加困难。
为了降低重构难度,你可以尝试分析构成模式的子模式。例如,你帮助孩子用乐高拼装好消防车,他可能惊叹于成品现在的样子,但如果你给孩子一桶积木,他就可以以不同方式拼装出各式各样的作品。
给你一个L形的几何图形,请你将它分成4份,要求每份的尺寸、形状和面积必须完全一致。
你可能会尝试下图下方的分割方式。这显然不符合要求,因为拆分后的图形只是形状相同,但尺寸不同。

正确答案如下图所示,原始图形被分成4块小的L形图形。得出答案的简单的方法是,先将原始图形分成三个正方形,再将每个正方形分成4份,也就是将整个形状分成12份,再按3个一组的方式重新组合,就能按要求将原始图形分成4份。

从某个角度讲,语言的全部意义就是提供了各自独立的单元,这些单元能以不同方式、不同顺序进行组合。但很快,这些方式本身就被确定为固定单元,不再是其他单元的临时组合。
任何事物都可以先分解为部分,再以全新的方式组合在一起,最终达到重组的目的。
请注意,你的目的不是寻找事物真实的组成部分,而是创造新的组成部分。天然的分割方式通常不太有效,因为拆分而成的部分重新拼凑起来,仍然摆脱不了原始模式。所以你需要以非天然的方式进行分割,以新的方式将单元组合起来。为实现这一目的,任何形式的分割都是可接受的。
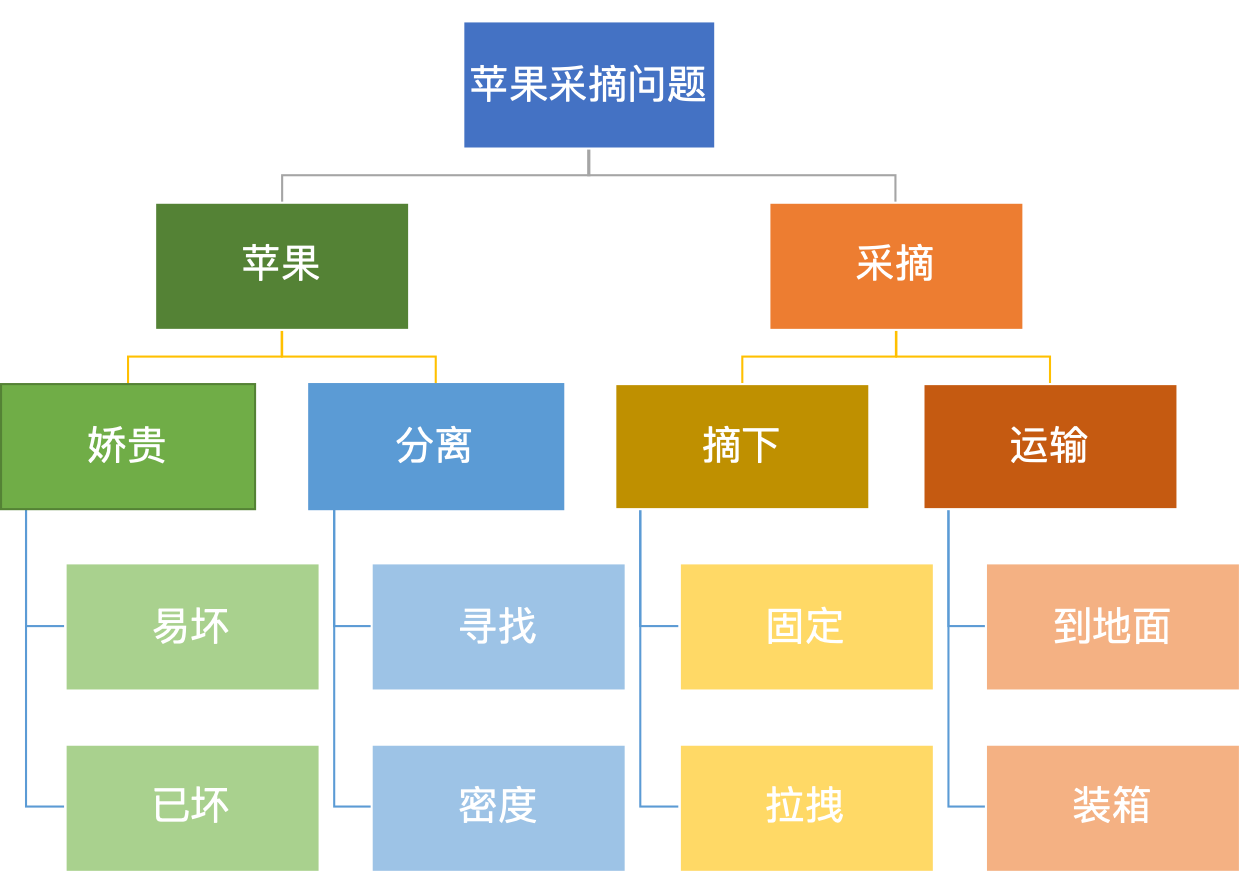
例如,前文提到的设计苹果采摘机的问题,可以拆分为以下部分:
-
够到苹果。
-
找到苹果。
-
摘下苹果。
-
将苹果运到地面。
-
保证苹果完好无损。
将它们重新组合时,有人可能将“够到苹果”、“找到苹果”、“摘下苹果”组合在一起,然后用“晃动果树”来代表这一组合。接下来就只剩一个问题:如何完好无损地将苹果运往地面。还有人可能将“够到苹果”与“保证苹果完好无损地运往地面”这两个部分组合起来,设计出用来接住苹果的可升降帆布平台。
你还可能以另一种方式来分解问题:
-
针对摘苹果这一问题,从树的角度能做些什么。
-
针对摘苹果这一问题,从果实角度能做些什么。
-
针对摘苹果这一问题,从机器的角度能做些什么。
从这一特定分解方式出发,就会设法以特定方式种植果树,以方便采摘。
既然分解的目的是打破固定模式的牢固整体,而不是提供描述性的分析,所以即使各部分未能覆盖整体状况,也是没关系的。只要能得到处理的素材,只要能重新组合信息、启发原始模式的重构,就已足够。同样地,分解出的各部分之间是否重合也不重要。
例如,“公交车客运”问题,可以分解如下:
-
路线选择。
-
发车频率。
-
便利程度。
-
选乘这一线路的乘客数量。
-
不同时间选乘该线路的乘客数量。
-
车辆大小。
-
经济效益与成本。
-
其他出行方式。
-
不得不选乘该线路的乘客数量,以及运行后愿意选乘该线路的乘客数量。
很明显,分解而来的各部分无法完全割离,某种程度上是相互重合的。比如,便利程度与路线选择、发车频率、甚至车辆大小都有关系。
很多时候,拆分问题可能很困难。这时,二分法很管用。你可以人为地将问题分解成两个单元,拆分的两部分再一分为二,以此类推,直至达到满意的数量。
二分法非常刻意,可能忽略了重要因素,但它的好处在于:找两个组成部分,比找几个部分要容易得多。
二分法并非必须将问题拆分成两个相等的部分,两个部分无论多不对等都无所谓。分割方式也不必遵循事物天然的组成方式。
例如,用二分法解决苹果采摘问题,分解过程可以如下。
最后,给你布置一个练习。你可以从以下问题中选择一个:
-
轮船装货。
-
餐厅用餐。
-
捕鱼与卖鱼。
-
组织足球联赛。
-
修建桥梁。
题目的要求是:
-
将问题进行分解,形成清单。分解方式不限。
-
从获得的清单中,将部分重新组合起来,形成看待问题的新方式。
-
将你的清单交给家人、朋友或同事,请他们分析你的清单在描述什么。如有可能,可以几个小组相互交换分解清单,分别猜测被分解的题目是什么。分解清单中如存在明显的线索,应予以删去,或用空格代替。
-
用二分法重新分解你的问题,并与之前的分解清单进行比较。
