水平思考的基本原则是:任何看待事物的方式,都只是众多可行方式中的一种。
水平思考的目的是:通过重新构建、重新编排现有信息,探讨看待问题的其他方式。
“水平”这个词说明:为了生成其他模式,你的思考方向应该向侧面发散,而不是抱着深化某一具体模式的目的一路纵深向前。
寻找看待事物的其他方式,似乎像一种自然行为,但沿水平方向寻找其他方案,绝不仅仅是一种自然行为:
-
自然寻找其他方式时,你寻找的对象是可行条件下的最佳方式;而水平寻找其他方式时,你需要尽可能多地找出一些不同的方式,也就是说你寻找的对象不是最佳方式,而是可行条件下最多样的方式。
-
自然寻找其他方式时,你找到一个有希望解决问题的方式就会停下来;水平寻找其他方式时,即便找到某个有希望的方式,最终可能就采用这一方式,但你还是会继续发掘更多的新方式。
-
自然寻找其他方式时,你只考虑合理的方式;水平寻找时,你不会局限于合理方式。
-
自然寻找其他方式通常只是一种意愿,不是事实;而水平寻找则是一种刻意的自发行为。
-
两者的主要区别体现在寻找其他方案的目的上。自然倾向下,寻找的目的是发现最好的方案;水平思考中,寻找的目的是解放刻板模式,启发新模式诞生。
为了练习你的水平思考能力,我带你做一些思维练习。
今天先用几何图形来练习。
几何图形的好处在于,材料的表现形态是明确的。不管你如何解读眼前的材料,并不会影响材料本身,材料始终保持不变。
标准化的几何图形,使用简单的词汇就能描述出来,你可以轻松地从一种描述跳到另一种描述,可以容易地描述观看图形的角度。
先提醒一下:我给你一个图形之后,你最好不要看下面的文字,先停下来思考一番。
练习一
给你一个这样的图形,你会如何描述它?需要你从不同的角度,提出多种答案。

你很容易想到,它是一个三角形放在长方形上面。
但经过一些思考,你也许会给出以下四种描述。
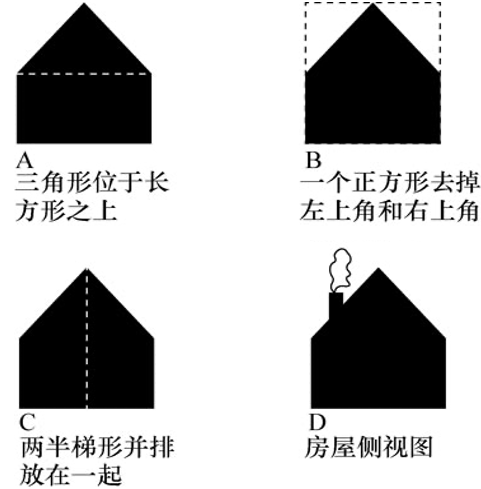
你还能想到更多的描述方案吗?你可以留言告诉我。
我鼓励和接受不同观点,越多越好,决不会加以批判。即使你的意见看起来有些离谱,我也不会指责你,只要你解释给大家。无论如何,我都不会驳斥你的任何观点。
练习二
你如何描述下面的的图形?
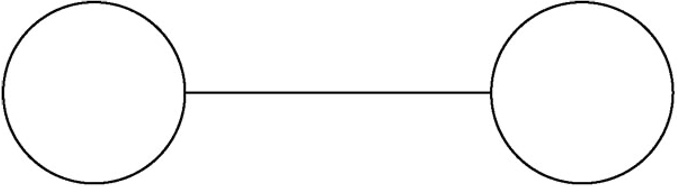
你肯定很容易说出:两个圆由一条直线连接。
你或许也能说出:
-
一条直线的两端各有一个圆。
-
有两个各带一条小尾巴的圆,摆放时保证两条尾巴在一条直线上,并连接在一起。
但你能够看出这样吗:一个沟槽倒扣在另一个上面。
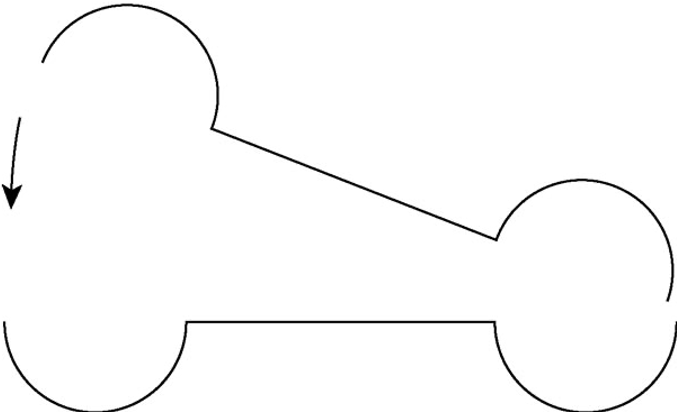
你可能质疑“两个圆由一条直线连接”与“一条直线的两端各有一个圆”两种说法是一样的,其实不是,因为前者的关注点一开始落在圆上,而后者则落在直线上。从大脑活动的角度讲,关注的顺序至关重要,关注顺序不同也构成不同观点。
有些描述可能是静态的,有些描述可能是动态的,要借助更多图示才能看清楚。
练习三
你如何描述下面的图形?

你可能能够想到这样一些不同看法:
-
L形。
-
木匠的角尺。
-
倒置的吊架。
-
只剩下一半的镜框。
-
两个长方形紧靠在一起。
-
一个大长方形挖去一个小长方形。
将这个图形描述为“木匠用的角尺”等实物,可能会有些麻烦,因为这种描述会开启无穷无尽的描述方式。比如,图形也可以被描述为一栋建筑的俯瞰图。你要明确认识到,题目的要求是以不同的方式描述图形,不是问图形可能是什么物体,也不是问图形让你联想到什么。你必须能让听者根据你所做的描述把图形画出来。因此,“图形看起来像建筑的俯瞰图”这种说法是没有任何意义的,除非事先指明建筑本身是L形的,但这和图形是“L形”的描述也就没有区别了。
你不要求描述高度精确,比如,“两个长方形紧靠在一起”的表述是应该交代方向的,但你没必要咬文嚼字,因为这样会弄错重点。
有些描述会表明具体的过程。比如,“两个长方形紧靠在一起”或“一个大长方形挖去一个小长方形”这样的描述实际上要求听者先联想到其他图形,然后在其他图形的基础上删减或改动。这种描述方法显然合理,基本描述类型包括:
-
将小单位组合。
-
与另一图形比较。
-
通过增减改变另一图形。
和前述情形一样,这种情况也需要其他图示的辅助来表现要描述的含义。
练习四
你如何描述下面的的图形?
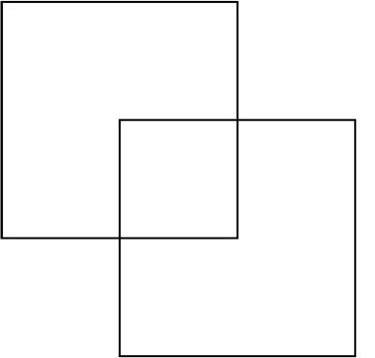
你可以有以下不同观点:
-
两个部分重合的正方形。
-
三个正方形。
-
两个L形图形摆在一起,形成一个正方形缺口。
-
一个长方形一分为二,将分成的两块图形推离同一条直线。
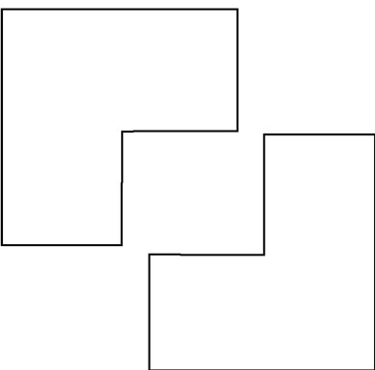
显然,“两个部分重合的正方形”是最明显的描述,它让其他描述听起来违反常理,这说明显而易见的模式在大脑中占据强大的优势地位。
你可能觉得“两个部分重合的正方形”和“三个正方形”的说法是一样的,因为后者可由前者推导而来。但你要克制这种倾向,因为即便稍稍改变看待事物的方式,也常常带来很大不同。你必须抵制住诱惑,不能仓促地判定一种描述在含义上等同于另一描述,进而将其归为文字游戏。
有些描述可能会细致到足以全面覆盖所有可能性:“两个正方形一角重合,重合部分也是正方形,该正方形的边长为初始正方形边长的一半。”如此全面的描述几乎能让听者精准地画出图形,所以它肯定囊括了各类其他描述。但你必须接受,其他描述也是独立的描述。从逻辑上讲,可由另一描述推导而来的描述是多余的。但从认知上讲,即便是同样的描述也可以采用新模式。所以,“三个正方形”的观点是有意义的,即便它隐含在“两个正方形部分重合”的描述中。
这样的练习,有意思吗?你也可以尝试开动脑筋,自己玩一玩。
下次我们继续练习。
