上一篇,我介绍了4个水平思考的几何图形练习,你有没有脑洞大开?你需要经常进行这样的锻炼。
今天继续介绍几何图形练习。不过,今天就要复杂一点了。
练习五
下图的图案是如何组成的?或者说,它的基本单元是什么?

注意,你需要用水平思考法考虑更多的情形,而不能停留于“它是由正方形方块组成的”这样的直接和浅薄看法。
略加观察,你能发现,它是由一个小正方形四周围绕大正方形,或一个大正方形四角围绕小正方形组成的。
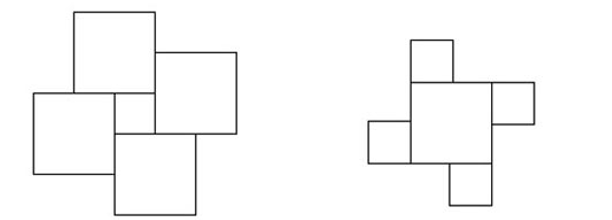
还有别的视角么?哦对,你能看出:
-
一排大正方形顺次排列,形成阶梯图案。
-
由一大一小两个正方形组成一个基本单位。
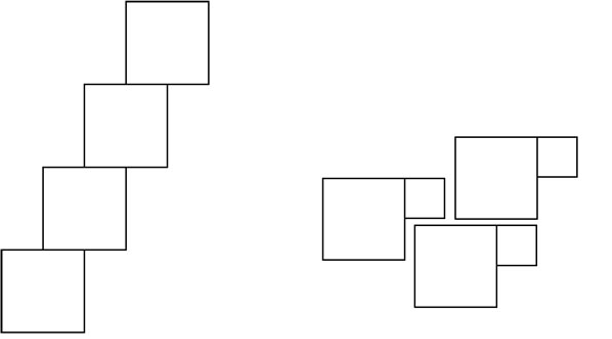
请继续。你还能想到什么方案?我稍微动动脑,能看出这样的:
-
将小正方形的四边延长,基于这些延长的边画四个小正方形。
-
将一条直线三等分,过各三等分点画垂线。
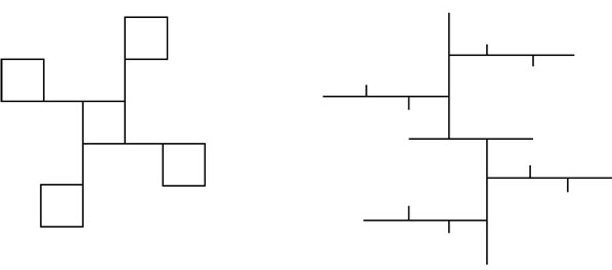
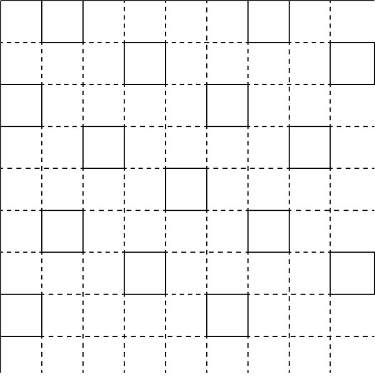
不过,如果不“偷看答案”,我看不出来这样的方案:网格图形中以特定方式选出部分小正方形勾勒边框,之后将边框线擦掉并用大正方形填充空间,然后,大正方形紧邻摆放,相邻两正方形有一半边长重合;两个重叠线条图案,一个图案与另一个图案呈直角。
其实,除了上述描述之外,你可能还能想到很多其他描述方式。但要注意,描述必须是有效的,必须能清晰地表明观察图案的角度。你要重点关注的是解构图案的不同方式,着眼点可以是大正方形、小正方形、大正方形和小正方形、直线、空间及网格图案。
练习六
如何将一个正方形四等分?
这个问题看上去很简单,你很容易能想到:
-
纵向等分。
-
分成四个小正方形。
-
沿对角线切分。

你可能比较不容易想到:
-
先将正方形分为十六个小正方形,再组合成“卍”字形或L形。
-
用小正方形的角作斜线,也能切分四等分。

你更难想到:用弧线切分,或其他“怪人”才能想到的切分方法。

一开始,你可能会将思路限制在纵向等分、沿对角线切分和分成四个小正方形这种简单方法。
之后,一旦你发现将大正方形分成十六个小正方形,再以不同方式组合,你就会会发现一个“原理”:连接正方形一边某点及对边某点的直线,如果两个点对两条对边的分割是一样的,则该直线将正方形等分;换到垂直方向上以相同方式连线,就可以将正方形四等分。显然,这种方式可以分割出的图形是无限的。你可以基于这一原理提出各种分割方法,却没有注意到背后的原理,而发现原理之后,你还可以在这一原理基础上稍加改动:先将正方形一分为二,再将每半份各自一分为二。就每个半份而言,如果穿过中心的分割线两侧图形完全对等,则分割方法符合条件。从这一思路出发能衍生出各种各样的图形。
请注意,这练习不是几何作业或设计作业,练习的目的不是探讨分割图形的所有可行方式,而是借此证明,当你以为已经穷尽所有可能性时,往往还有更多其他方法等待发现。
练习七
如何将正方形纸板剪开(最多可以剪两刀),组成和正方形面积相等的L形?
你很容易想到:将正方形剪成两个长方形。
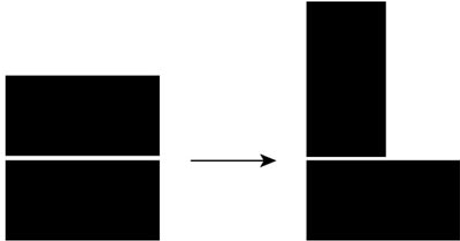
“最多剪两刀”的要求,相当于加入了限制条件。这不是为了约束你的思路,而是为了鼓励你不满足于简单的解决方案,进一步挖掘其他复杂的方法。
例如,你或许能想到:从大正方形中剪下一个小正方形。
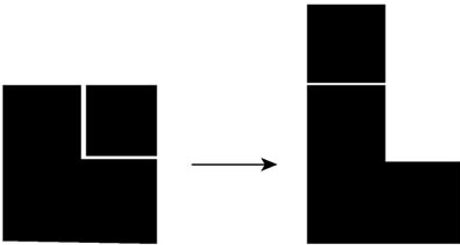
一般来说,你会比较习惯用水平线、竖直线或直角来分割图形,不太容易发现沿对角线分割的方法。
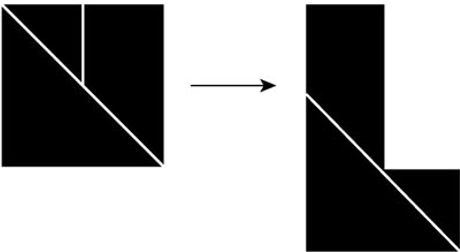
要发现这种方法,最好的办法也许是:先沿对角线将正方形剪开,看看是什么结果。
实际上,这样的做法,已经超越了简单的分析性行为,开始升级为启发性行为了。
下一次,我带你继续练习。但就不再用几何图形了。
